Marketing Attribution - Sharpley Value Approach

Bernard Yeo
@byeothoughts

In online advertising, evaluating media effectiveness is an important part during the media investment decision-making process. With cost being charged for every clicks and impression, it is important that we understand the marketing effect of the different channels by asking ourselves “what is the contributions my marketing channels has when it comes to conversion?"

With this question in mind, we are going to touch on marketing attribution, something that we might have come across at some point in our digital marketing journey.

While the content will get technical at times, I’ll try to break it down so that we can get the intuition behind the model.

THE CUSTOMER JOURNEY

An example of a customer journey: Bernard begins his journey by clicking on a sponsored ad on Facebook that redirects him to the Skyscanner’s website. He then comes across an ad banner the following day, which he clicks on as well. Eventually, a search ad finally convinced him to go purchase ticket on Skyscanner’s website. This multi-touch journey that a customer takes before converting (making a purchase on Skyscanner) is common within the e-commerce industry.

Now you may then be asking, which of these touchpoint should get the credits for converting the customer?

“Marketing attribution is the process of assigning the credit of a purchase (or any other action of interest, such as subscribing to a newsletter or downloading some content — this is what we call a conversion) to the right marketing channels, given all the channels that the customer interacted with prior to the purchase."

RULE-BASED vs. ALGORITHMIC

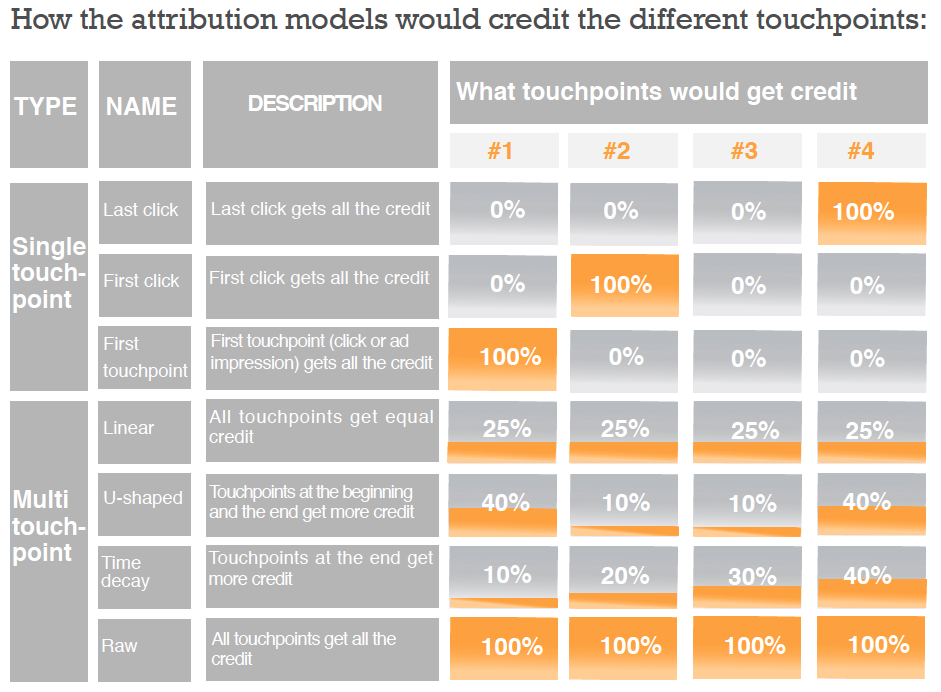
A widely used attribution model within the industry is Last Click Attribution, where we give the last paid touchpoint the full credit. While Last Click Attribution helped us learn a little bit more about the situation, it is still not enough as we are being biased and not giving credit to the prior touchpoints which played a part in getting the conversion. This then brings about the development of other attribution models shown in the table above.

A common limitation about these models is that attributions are based on a set of rules (eg. last channel should get the credit, all channel get equal credits, etc.) rather than exploring the correlation between the channels and conversion.

With the growth of big data & computational power, we are now in a better position to design a data driven attribution model, without user-defined rules. While there are many data driven choices, two notable options stood out, Shapley Value Attribution and Markov-Chain Attribution. In this post, I will be going over the implementation of Shapley Value Attribution, which is part of Game theory. Shapley Value Attribution is also the approached used by Google Analytics Data-Driven Attribution model.

COOPERATIVE GAME THEORY

“Non-Cooperative Games covers competitive social interactions where there will be some winners & some losers, and in Cooperative Games, every player agreed to work together a common goal."

Game theory is a study of mathematical models of strategic interaction among rational decision-makers (players). There are two main branches within Game theory, Cooperative and Non-Cooperative. In this post, we will be touching on Cooperative Games theory.

A coalition is what you call a group of players in a Cooperative Games theory. When it comes to Cooperative Games, Game theory main question is how much each player should contribute to the coalition and how much they should benefit from it (in other words, trying to determine what is fair). This bring us to Shapley value, a method of dividing up gains or costs among players according to the value of their individual contributions when they work in cooperation with each other to obtain the payoff.

In marketing context, this means marketing channels are the players in the cooperative game and each of them can be thought of as working together in order to drive conversions (payoff). Shapley value approach aims to fairly assigns each touchpoint contribution to the conversion.

When it come to fair attribution of the total number of conversions among all the channels involved, this axiomatized in the following rules:

Marginal Contribution

Contribution of each player is determined by what is gained or lost by removing them from the game.
Interchangeable Players have Equal Value

Players who always contribute with the same amount to every coalition should receive the same allocations.
Dummy Players have Zero Value

If the contribution of a player to any coalition is always equal to the payoff that he can generates alone, then this player should receive the amount that he can achieve on his own.
If a Game has Multiple Parts, Cost or Payment should Decomposed across those Parts

Having weights assigned to the cost or payment, based on the contribution made at various points. This means making adjustments regularly to the coalition based on the players contribution in those specific scenarios.

Takeaway

In game theory, the Shapley value is a solution concept of fairly distributing both gains and costs to several actors working in coalition.

The Shapley value applies primarily in situations when the contributions of each actor are unequal, but they work in cooperation with each other to obtain the payoff.

MULTI-TOUCH ATTRIBUTION MODEL USING SHAPLEY VALUE

Using Kaggle marketing dataset (data), we will extract the following four variables: ‘user_id’, ‘date_served’, ‘marketing_channel’, ‘converted’. Some pre-processing work is done to drop rows which contain null values, as well as relabel ‘converted’ into binary.

###  extracting the needed field
columns = ['user_id', 'date_served', 'marketing_channel', 'converted']
data = data_raw[columns].copy()

### dropping null values
data.dropna(axis=0, inplace=True)

### relabel conversion to 1/0
data['converted'] = data['converted'].astype('int') 
### converting date_served into date format
data['date_served'] = pd.to_datetime(data['date_served'], format='%m/%d/%y', errors='coerce')

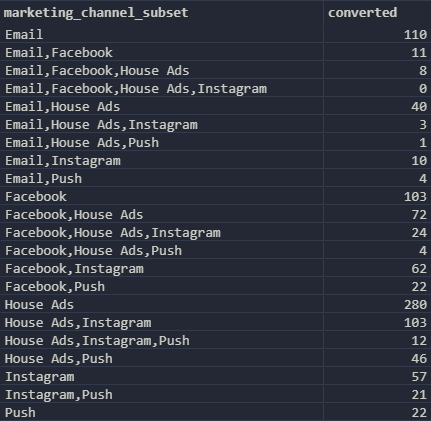
In the first step of the calculation, we will compute for each channel subset, the sum of conversions generated.

### create a channel mix conversion table 
# first level - sort
data_lvl1 = data[['user_id', 'marketing_channel', 'converted']].sort_values(by=['user_id', 'marketing_channel'])

# second level - groupby userid, concat distinct marketing channel and label if any conversion took place with this channel mix
data_lvl2 = data_lvl1.groupby(['user_id'], as_index=False).agg({'marketing_channel': lambda x: ','.join(map(str,x.unique())),'converted':max})
data_lvl2.rename(columns={'marketing_channel':'marketing_channel_subset'}, inplace=True)

# third level - summing up the conversion which took place for each channel mix
data_lvl3 = data_lvl2.groupby(['marketing_channel_subset'], as_index=False).agg(sum)

The output will look like this:

Once we have prepared the dataset, we will then proceed to write a function that returns all the possible channel combinations.

### return all possible combination of the channel
def power_set(List):
    PS = [list(j) for i in range(len(List)) for j in itertools.combinations(List, i+1)]
    return PS

Next we will then set up another function that returns all possible channel subsets, together with the its conversions worth. This is where the combination will expand exponentially, as each coalition will be broken down into a list of subsets. (e.g. if A={a,b,c}, then the function would return the list [{a},{b},{c},{ab},{ac},{bc},{abc}])

### return all possible subsets from the channels
def subsets(s):
    '''
    This function returns all the possible subsets of a set of channels.
    input :
            - s: a set of channels.
    '''
    if len(s)==1:
        return s
    else:
        sub_channels=[]
        for i in range(1,len(s)+1):
            sub_channels.extend(map(list,itertools.combinations(s, i)))
    return list(map(",".join,map(sorted,sub_channels)))

################################################################################

### compute the worth of each coalition
def v_function(A,C_values):
    '''
    This function computes the worth of each coalition.
    inputs:
            - A : a coalition of channels.
            - C_values : A dictionnary containing the number of conversions that 
            each subset of channels has yielded.
    '''
    subsets_of_A = subsets(A)
    worth_of_A=0
    for subset in subsets_of_A:
        if subset in C_values:
            worth_of_A += C_values[subset]
    return worth_of_A

We can then compute the Shapley value for each channel using the below function.

### calculate shapley value
def calculate_shapley(df, channel_name, conv_name):
    '''
    This function returns the shapley values
            - df: A dataframe with the two columns: ['channel_name', 'conv_name'].
            The channel_subset column is the channel(s) associated with the conversion and the 
            count is the sum of the conversions. 
            - channel_name: A string that is the name of the channel column 
            - conv_name: A string that is the name of the column with conversions
            **Make sure that that each value in channel_subset is in alphabetical order. 
            Email,PPC and PPC,Email are the same in regards to this analysis and 
            should be combined under Email,PPC.            
    '''
    # casting the subset into dict, and getting the unique channels
    c_values = df.set_index(channel_name).to_dict()[conv_name]
    df['channels'] = df[channel_name].apply(lambda x: x if len(x.split(",")) == 1 else np.nan)
    channels = list(df['channels'].dropna().unique())
    
    v_values = {}
    for A in power_set(channels): #generate all possible channel combination
        v_values[','.join(sorted(A))] = v_function(A,c_values)
    n=len(channels) #no. of channels
    shapley_values = defaultdict(int)

    for channel in channels:
        for A in v_values.keys():
            if channel not in A.split(","):
                cardinal_A=len(A.split(","))
                A_with_channel = A.split(",")
                A_with_channel.append(channel)            
                A_with_channel=",".join(sorted(A_with_channel))
                weight = (factorial(cardinal_A)*factorial(n-cardinal_A-1)/factorial(n)) # Weight = |S|!(n-|S|-1)!/n!
                contrib = (v_values[A_with_channel]-v_values[A]) # Marginal contribution = v(S U {i})-v(S)
                shapley_values[channel] += weight * contrib
        # Add the term corresponding to the empty set
        shapley_values[channel]+= v_values[channel]/n 
        
    return shapley_values

Using the dataset, we will now generate the Shapley value for each channel and visualizing it on a chart.

### calculating the shapley value of the channel
shapley_dict = calculate_shapley(data_lvl3, 'marketing_channel_subset', 'converted')

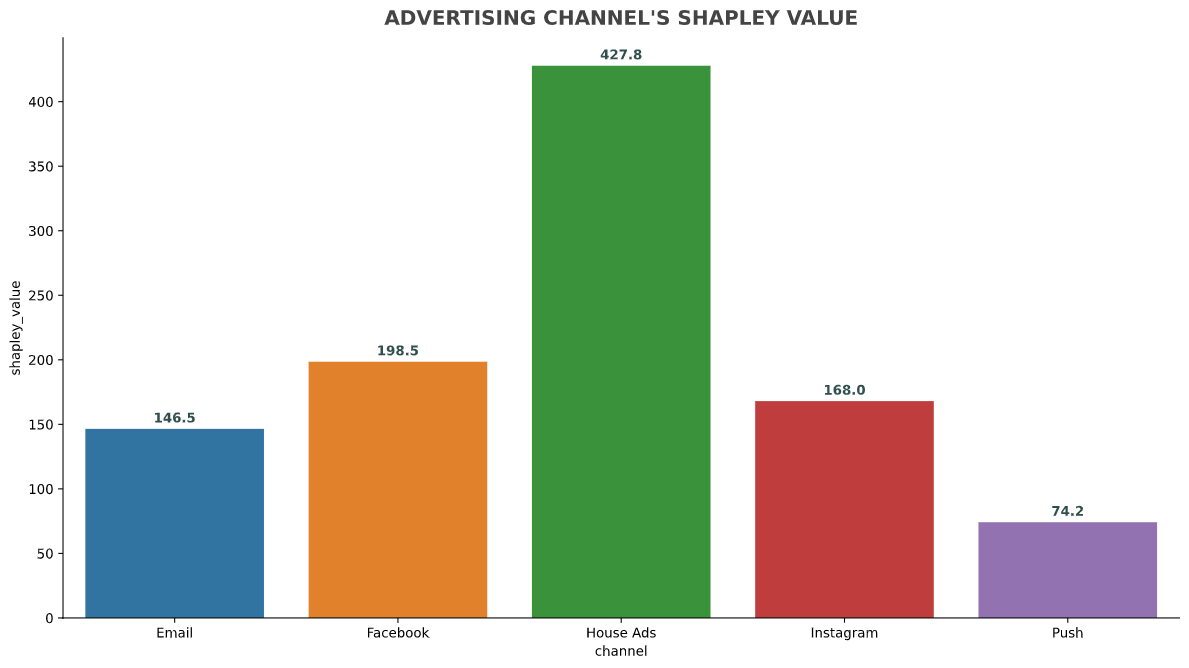
On the Y-axis, we see each channel’s attribution towards the total number of conversions where it is accountable for. (bearing in mind that a converted user may not be exposed to all channel before converting) The sum of all the channel’s attribution value will equals to the total conversion found in the dataset.

From the chart, we see that house ads received the most credit when it comes to conversion. We may then want to allocate more resources or expand more audience towards it so as to improve conversions.

You can head over to my Github for the Python implementation of the above Shapley value attribution model.

AFTER THOUGHTS

In the calculation of the Shapley value, the channels coalition does not take the sequential effect of channels into account. So all the users who visited channels A and B (in whichever order) would share the same coalition (coalition {A,B} for example). The sorting of and aggregation of ‘data_lvl1’ and ‘data_lvl2’ enforce a particular order (in this case, an alphabetical order) for channels in a coalition.

Shapley value does well up to 10-15 channels, after that it become exponentially complicated to compute the payoffs.

This post is an overview of Shapley value and Python implementation with the help from various sources. In the near future I will update this post to show how Shapley value differ from existing rule-based attribution as well as how Shapley value would differ when I add in channel exposure sequence.